訓練智能體¶

本頁簡要概述如何為 Gymnasium 環境訓練智能體，特別是，我們將使用基於表格的 Q-learning 來解決 Blackjack v1 環境。如需本教學的完整版本以及其他環境和演算法的更多訓練教學，請參閱此處。在閱讀本頁之前，請先閱讀基本用法。在我們實作任何程式碼之前，以下是 Blackjack 和 Q-learning 的概述。

Blackjack 是最受歡迎的賭場紙牌遊戲之一，也因在某些條件下可被擊敗而臭名昭著。此版本的遊戲使用無限牌組（我們抽牌時會放回牌堆），因此在我們的模擬遊戲中，算牌不是一個可行的策略。觀察結果是玩家當前總和、莊家明牌的值以及玩家是否持有可用 A 的布林值的元組。智能體可以在兩個動作之間選擇：停牌 (0)，表示玩家不再拿牌；以及叫牌 (1)，表示玩家將再拿一張牌。為了獲勝，您的牌總和應大於莊家，且不超過 21 點。當玩家選擇停牌或牌總和超過 21 點時，遊戲結束。完整文件請參閱https://gymnasium.dev.org.tw/environments/toy_text/blackjack。

Q-learning 是 Watkins 於 1989 年提出的一種用於離散動作空間環境的免模型離策略學習演算法，並以成為第一個證明在特定條件下收斂到最佳策略的強化學習演算法而聞名。

執行動作¶

在收到我們的第一個觀察結果後，我們只會使用env.step(action)函數與環境互動。此函數將動作作為輸入，並在環境中執行它。由於該動作會改變環境的狀態，因此它會向我們返回四個有用的變數。這些是

next observation：這是智能體在採取動作後將收到的觀察結果。
reward：這是智能體在採取動作後將收到的獎勵。
terminated：這是一個布林變數，指示環境是否已終止，即由於內部條件而結束。
truncated：這也是一個布林變數，指示回合是否因提前截斷而結束，即達到時間限制。
info：這是一個字典，可能包含有關環境的其他資訊。

next observation、reward、terminated 和 truncated 變數是不言自明的，但 info 變數需要一些額外的解釋。此變數包含一個字典，其中可能包含有關環境的一些額外資訊，但在 Blackjack-v1 環境中，您可以忽略它。例如，在 Atari 環境中，info 字典有一個 ale.lives 鍵，告訴我們智能體還剩下多少條命。如果智能體的命數為 0，則回合結束。

請注意，在您的訓練迴圈中呼叫 env.render() 並不是一個好主意，因為渲染會大大減慢訓練速度。而是嘗試建立一個額外的迴圈，在訓練後評估和展示智能體。

建立智能體¶

讓我們建立一個 Q-learning 智能體來解決 Blackjack！我們需要一些函數來選擇動作並更新智能體的動作值。為了確保智能體探索環境，一種可能的解決方案是 epsilon-greedy 策略，我們以 epsilon 的百分比選擇隨機動作，以及貪婪動作（目前評估為最佳）1 - epsilon。

from collections import defaultdict
import gymnasium as gym
import numpy as np


class BlackjackAgent:
    def __init__(
        self,
        env: gym.Env,
        learning_rate: float,
        initial_epsilon: float,
        epsilon_decay: float,
        final_epsilon: float,
        discount_factor: float = 0.95,
    ):
        """Initialize a Reinforcement Learning agent with an empty dictionary
        of state-action values (q_values), a learning rate and an epsilon.

        Args:
            env: The training environment
            learning_rate: The learning rate
            initial_epsilon: The initial epsilon value
            epsilon_decay: The decay for epsilon
            final_epsilon: The final epsilon value
            discount_factor: The discount factor for computing the Q-value
        """
        self.env = env
        self.q_values = defaultdict(lambda: np.zeros(env.action_space.n))

        self.lr = learning_rate
        self.discount_factor = discount_factor

        self.epsilon = initial_epsilon
        self.epsilon_decay = epsilon_decay
        self.final_epsilon = final_epsilon

        self.training_error = []

    def get_action(self, obs: tuple[int, int, bool]) -> int:
        """
        Returns the best action with probability (1 - epsilon)
        otherwise a random action with probability epsilon to ensure exploration.
        """
        # with probability epsilon return a random action to explore the environment
        if np.random.random() < self.epsilon:
            return self.env.action_space.sample()
        # with probability (1 - epsilon) act greedily (exploit)
        else:
            return int(np.argmax(self.q_values[obs]))

    def update(
        self,
        obs: tuple[int, int, bool],
        action: int,
        reward: float,
        terminated: bool,
        next_obs: tuple[int, int, bool],
    ):
        """Updates the Q-value of an action."""
        future_q_value = (not terminated) * np.max(self.q_values[next_obs])
        temporal_difference = (
            reward + self.discount_factor * future_q_value - self.q_values[obs][action]
        )

        self.q_values[obs][action] = (
            self.q_values[obs][action] + self.lr * temporal_difference
        )
        self.training_error.append(temporal_difference)

    def decay_epsilon(self):
        self.epsilon = max(self.final_epsilon, self.epsilon - self.epsilon_decay)

訓練智能體¶

為了訓練智能體，我們將讓智能體一次玩一個回合（一個完整的遊戲稱為一個回合），並在每個回合中採取的每個動作後更新其 Q 值。智能體將必須體驗大量回合才能充分探索環境。

# hyperparameters
learning_rate = 0.01
n_episodes = 100_000
start_epsilon = 1.0
epsilon_decay = start_epsilon / (n_episodes / 2)  # reduce the exploration over time
final_epsilon = 0.1

env = gym.make("Blackjack-v1", sab=False)
env = gym.wrappers.RecordEpisodeStatistics(env, buffer_length=n_episodes)

agent = BlackjackAgent(
    env=env,
    learning_rate=learning_rate,
    initial_epsilon=start_epsilon,
    epsilon_decay=epsilon_decay,
    final_epsilon=final_epsilon,
)

資訊：目前的超參數設定旨在快速訓練出一個像樣的智能體。如果您想收斂到最佳策略，請嘗試將 n_episodes 增加 10 倍，並降低 learning_rate（例如降至 0.001）。

from tqdm import tqdm

for episode in tqdm(range(n_episodes)):
    obs, info = env.reset()
    done = False

    # play one episode
    while not done:
        action = agent.get_action(obs)
        next_obs, reward, terminated, truncated, info = env.step(action)

        # update the agent
        agent.update(obs, action, reward, terminated, next_obs)

        # update if the environment is done and the current obs
        done = terminated or truncated
        obs = next_obs

    agent.decay_epsilon()

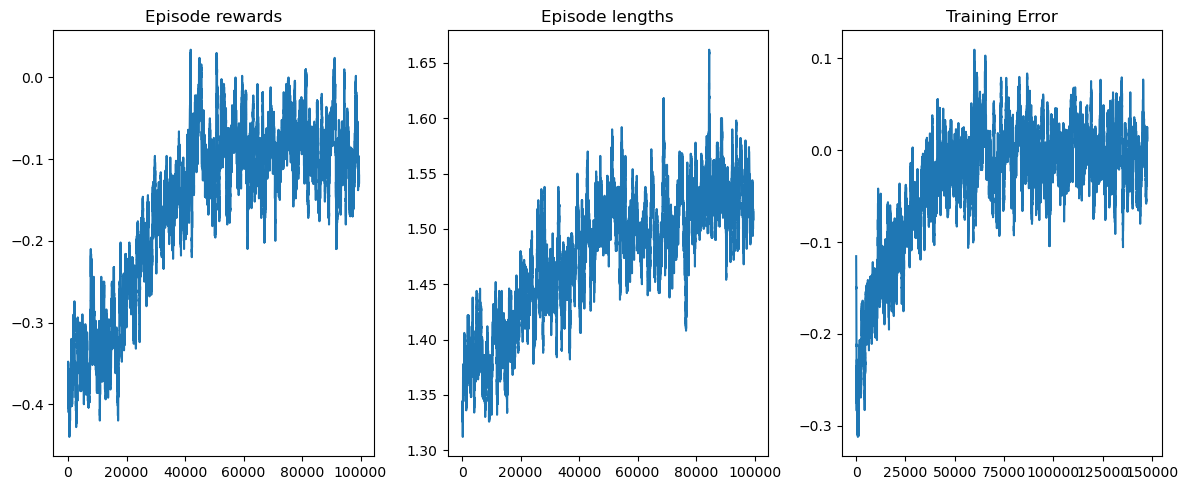
您可以使用 matplotlib 來視覺化訓練獎勵和長度。

from matplotlib import pyplot as plt

def get_moving_avgs(arr, window, convolution_mode):
    return np.convolve(
        np.array(arr).flatten(),
        np.ones(window),
        mode=convolution_mode
    ) / window

# Smooth over a 500 episode window
rolling_length = 500
fig, axs = plt.subplots(ncols=3, figsize=(12, 5))

axs[0].set_title("Episode rewards")
reward_moving_average = get_moving_avgs(
    env.return_queue,
    rolling_length,
    "valid"
)
axs[0].plot(range(len(reward_moving_average)), reward_moving_average)

axs[1].set_title("Episode lengths")
length_moving_average = get_moving_avgs(
    env.length_queue,
    rolling_length,
    "valid"
)
axs[1].plot(range(len(length_moving_average)), length_moving_average)

axs[2].set_title("Training Error")
training_error_moving_average = get_moving_avgs(
    agent.training_error,
    rolling_length,
    "same"
)
axs[2].plot(range(len(training_error_moving_average)), training_error_moving_average)
plt.tight_layout()
plt.show()

希望本教學能幫助您掌握如何與 Gymnasium 環境互動，並引導您踏上解決更多 RL 挑戰的旅程。

建議您自行解決此環境（基於專案的學習非常有效！）。您可以應用您最喜歡的離散 RL 演算法，或嘗試 Monte Carlo ES（在 Sutton & Barto <http://incompleteideas.net/book/the-book-2nd.html>_，第 5.3 節中介紹） - 這樣您就可以將您的結果直接與本書進行比較。

祝您好運！